how to use a parabola for multiplication

It's possible to multiply any two real numbers using just a parabola and some straight lines. Pick two numbers, x₁ and x₂ say, extend a line vertically until you hit the parabola, join both of these points and where this line intersects the y-axis, is the product -ax₁x₂, where a is the coefficient of the x² term in the parabola.

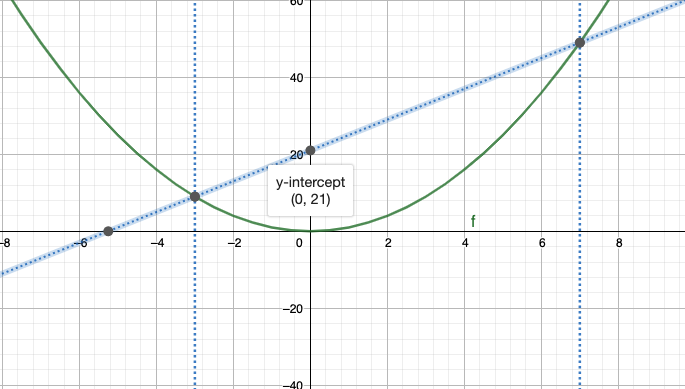
In the example below, I choose x₁ = 7 and x₂ = -3, and a parabola described by y = x².
As you can see, the line joining points (-3,9) and (7,49) intersects the y-axis at (0,21), which is equal to -(1)(7)(3).

The choice of parabola is irrelevant here, as long as the constant term is 0. I will use the general from of a parabola with no constant term, that is y = ax²+bx, in the proof below to demonstrate this.

Proof:
Claim: The y-intersect of the line joining two points on a parabola described by y = ax²+bx is the negative of the product of the x components of the same two points on the parabola and the coefficient of the x² term describing the parabola.

Let x₁ and x₂ be two arbitrary points on the x-axis. Then, both

y₁ = ax₁²+bx₁
y₂ = ax₂²+bx₂

are points lying on the parabola, and the equation of the line joining them is given by l = mx+c, where m is the slope and is described by:

m = (1/x₁-x₂)(ax₁²+bx₁ - (ax₂²+bx₂))
m = (1/x₁-x₂)(ax₁²+bx₁ - ax₂²-bx₂)
m = (1/x₁-x₂)(a(x₁²-x₂²)+b(x₁-x₂))
m = (1/x₁-x₂)(a(x₁-x₂)(x₁+x₂)+b(x₁-x₂)) (Difference of squares)
m = a(x₁+x₂)+b

Therefore, the line l joining y₁ and y₂ on the parabola is given by l = (a(x₁+x₂)+b)x+c. It just remains to calculate the value of c, which is the y-intersect of l.

Since we already know that (x₁,ax₁²+bx₁) is a point on the parabola, filling these values into the equation of l, we get:

ax₁²+bx₁ = (a(x₁+x₂)+b)x₁+c
ax₁²+bx₁ = ax₁²+ax₁x₂+bx₁+c
0 = ax₁x₂+c
c = -ax₁x₂  

Note:
The parabola can't have a non-zero constant term, as this value would just shift the parabola up or down vertically, which would only affect the value of the y interesection. For more on parabolas, Matt Parker has a video on his youtube channel: There is only One True Parabola