can the knight fork them?
chess
I like playing chess, but I'm not very good at it. I particularly find the middle game hard, trying to improve my position without blundering the game in the process.
The knight is particularly useful in the middle-game, when there are still a lot of pieces on the board. The movement of the knight is the most difficult to visualise, (for myself at least) and so it's often overlooked in terms of it's attacking capabilities. It's very good at forking pieces and is the only piece that can fork the king and queen without being threatened itself. But these knight forks can be hard to see. One tactic I use is to calculate the area of the rectangle drawn out by two pieces.
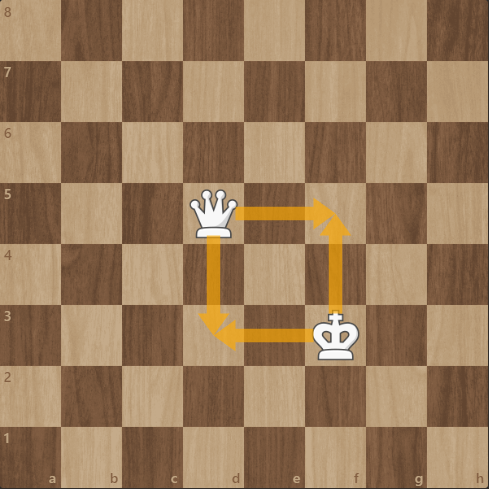
In this example, the area of the square drawn out by the king and queen is 9, and the knight can't fork them:
The area of the rectangle drawn out by 2 pieces can range between 2 and 64. (Our units here are chess board squares (cbs) and are not SI units. Use at your own peril.) But note that the maximum range in 1 dimension is 5 cbs and that the maximum area is 16 cbs squared. This allows us to exclude the following: 1. Areas with at least 1 dimension greater than 5 cbs 2. Areas greater than 16 cbs squared
The table below gives the remaining areas:
| area | width x height | can the knight fork them? | 2 | 1 x 2 | No |
|---|---|---|
| 3 | 1 x 3 | Yes |
| 4 | 1 x 4 | No |
| 4 | 2 x 2 | Yes |
| 5 | 1 x 5 | Yes |
| 6 | 2 x 3 | No |
| 8 | 2 x 4 | Yes |
| 9 | 3 x 3 | No |
| 10 | 2 x 5 | No |
| 12 | 3 x 4 | No |
| 15 | 3 x 5 | Yes |
| 16 | 4 x 4 | Yes |